Free GAMSAT Maths Tips and Formulas
While the GAMSAT Maths section does not exist in the real exam, Section 3 does have a few problems (particularly in GAMSAT Physics or GAMSAT Chemistry) that require basic mathematical skills or manipulations. Keep in mind that the GAMSAT March 2012 sitting was the first time ever that calculators were banned. Many students were surprised by the number of calculations they were required to perform on the real exam. So, is it possible to pass these GAMSAT Maths questions without the help of a calculator?
Well, if you are patient, you will learn that being efficient and using pattern recognition can be very powerful. You CAN actually make "magic" with numbers on the GAMSAT. Below are a few quick and useful tips and formulas to add to your GAMSAT Maths techniques.
* For advice on essential items to bring during the exam, please check out our forum on GAMSAT Test Day Items.
Tip #1: Spot patterns in GAMSAT Maths.
Have you seen these numbers on GAMSAT Physics or GAMSAT Chemistry exams: 1.44, 1.69? Do they ring a bell? You should have memorised all squares between 1 and 15. You likely have 1 to 10 stone cold! 11 squared is 121, 12 is 144, 13 is 169, 14 is 196, 15 is 225 . . . Test makers choose their numbers carefully. The moment you see 1.44 on the GAMSAT, there would be a high likelihood that taking the square root, which gives 1.2, would be required. Pattern recognition, yes?
Tip #2: Given A = sq root B.
Sometimes the GAMSAT will say, if B increases by 44%, by what % will A increase? Easy as pie! If B increases by 44%, that is the same as saying 1.44(B) and we know that root 1.44 is 1.2, which means the original sq root B = A has increased by 20%. (Of course, it's not a math test so they won't use "A" and "B" but rather they may present a physics equation to you). Even if they tell you, "given g = 9.8 m/s2," you use 10 unless the answers are very close to each other.
Tip #3: A little blast from the past
Pi is 3.14, root 2 is 1.4, root 3 is 1.7. Don't be surprised if you need to calculate the perimeter (2 pi r) or area (pi r squared) of a circle. Be comfortable estimating the root of anything! Root 17? Well, the answer must be between 4 and 5 but closer to 4! Check the answers and don't calculate anything if there is only one answer that is between 4 and 4.5.
Tip #4: Avoid decimals until you have no choice!
Fractions will usually permit you to be more efficient. For huge and tiny numbers, you need to be comfy with scientific notation. And if you can hang on to variables for as long as possible, that's even better. You may be surprised how many times mass m ends up being irrelevant as it happily cancels out!
Tip #5: Build on your stored knowledge.
Most past "gamsatters" felt that they rarely used their calculators for GAMSAT Maths. So relax! Be sure that you know the basics and work through all of ACER's practice materials without the use of a calculator and then math will not hold you back !
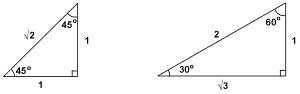
| sin θ = opp/hyp | cos θ = adj/hyp | tan θ =opp/adj |
| θ = sin-1 x | Estimate square root 3 as 1.7 and root 2 as 1.4 | r2 = x2 + y2 |
- Angle θ may be given in radians (R) where 1 revolution = 2πR = 360°
- Cross-sectional area of a tube = area of a circle = πr2 where π can be estimated as 3.14 and r is the radius of the circle; circumference = 2πr.
NB: If you happen to own the Gold Standard GAMSAT textbook then be sure to read Appendix A to review your GAMSAT Maths essentials such as basic graphs, significant figures, exponents/logarithms, etc.
Get 1 full hour access to free GAMSAT Physics and GAMSAT Chemistry and Biology videos online. Register here: Free GAMSAT-prep User Account
Helpful Links for GAMSAT Physics and GAMSAT Chemistry
 |
 |
 |
 |
|||||||||||
|
||||||||||||||